
이번 포스팅에서는 상미분·편미분·연쇄율 등 인공지능에 필요한 여러 가지 미분 관련 지식을 학습합니다.
미분은 한마디로 변화의 비율을 말합니다. 예를 들어 움직이는 물체의 위치를 시간으로 미분하면 그 물체의 속도가 됩니다.
인공지능에서는 다변수함수나 합성함수 등의 조금 복잡한 함수를 미분해야 합니다. 어렵게 느껴질 수도 있지만 이 장에서는 이것들을 하나하나 차근차근 설명합니다.
여러 가지 인공지능 기술의 배경이 되는 이론에 미분은 불가결한 것인데, 이 장에서는 미분의 기본부터 시작해서 다변수로 이뤄진 함수의 미분, 여러 개의 함수로 이뤄진 합성함수의 미분 등을 설명합니다.
복잡한 함수의 미분을 학습함으로써 어떤 파라미터가 전체에 미치는 영향을 예측할 수 있게 됩니다.
이 포스팅에서 미분 설명은 학문으로서의 수학인 경우의 엄밀성이 빠진 부분이 있습니다. 그러나 인공지능 학습에서는 미분에 대한 상상력을 키우는 것이 중요하므로 엄밀한 이해보다도 개념 파악을 중시해서 진행해 나갑시다.
극한의 개념 그리고 이를 기반으로 한 미분의 개념을 이해합시다. 미분은 어떤 함수상의각 점에서의 변화의 비율로 인공지능에서 자주 사용합니다.
- 극한
극한은 함수에서의 변수값을 어떤 값에 가깝게 할 때, 함수의 값이 한없이 가까워지는 값 을 말합니다.
예로서, 함수 y = x² + 1 에서 x를 점차 작게 해서 0에 가깝게 하는 경우를 생각합시다.
● x = 2일 때 y = 5
● x = 1일 때 y = 2
● x = 0.5일 때 y =1.25
● x = 0.1일 때 y = 1.01
● x = 0.01일 때 y = 1.0001
이처럼 x를 0에 가깝게 하면 y 는 1에 가까워집니다.
이것은 다음과 같이 식으로 나타낼 수 있습니다.
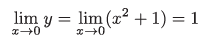
이 식은 「x를 한없이 0에 가깝게 하면, y가 한없이 1에 가까워진다」는 의미입니다.
- 미분
함수 y = f(x) 에서 x의 미소한 변화량을 x로 하면 x를 Δx만큼 변화시킬 때의 y 값은 다음과 같습니다.

이 때, y의 미소한 변화량은 다음과 같습니다.

따라서, y의 미소한 변화 Δy와 x의 미소한 변화 Δx의 비율은 다음 식으로 표현합니다.
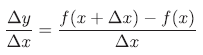
이 식에서 Δx의 값을 0에 한없이 가까워지는 극한을 생각합니다.
이 극한은 새로운 함수 f'(x) 로서 나타낼 수 있습니다.
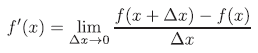
이 함수 f'(x)를 f(x)의 도함수라고 합니다. 그리고 함수 f(x)로부터 도함수 f'(x)를 얻는 걸 함수 f(x)를 미분한다고 합니다.
도함수는 다음과 같이 표기할 수도 있습니다.
이 경우는 함수의 변수가 x뿐인데, 이와 같은 1변수 함수에 대한 미분을 상미분이라고 합니다.
이 책에서는 x에 대한 y의 변화 비율을 기울기(경사, 그라디언트, 구배)라고 부르는데, 도함수에 의해 1변수 함수 상의 어떤 점에서의 기울기를 구할 수 있습니다.
함수 f(x)상의 어떤 점, (a, f(a))에서의 기울기는 f'(a)가 됩니다.
이 관계를 아래 그림으로 나타냅니다.
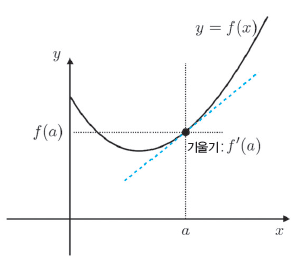
위 그림에서 기울어진 파선은 곡선상의 점 (a, f(a))에서의 접선입니다. 그 접선의 x에 대한 y 의 변화율, 즉, 기울기는 f'(a)이며, 곡선상의 이 점에서 국소적인 기울기와 같아집니다.
또한, 이 접선의 식은 다음과 같습니다.
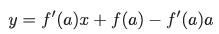
x에 a를 대입하면 y가 f(a)와 같아지는 것을 확인할 수 있습니다.
- 미분 공식
몇 가지 함수는 미분의 공식을 이용함으로써 간단하게 도함수를 구할 수 있습니다.
다음에 미분 공식 몇 가지를 소개합니다. 각 공식의 증명은 여기서는 하지 않으므로 흥미 있는 분은 각자 살펴봅시다.
r을 임의의 실수로서 f(x)=x² 로 했을 때, 다음이 성립됩니다.
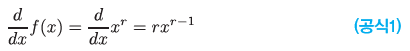
또한, 함수의 함 f(x) + g(x)를 미분할 때는 각각을 미분해서 더합니다.

함수의 곱 f(x)g(x)는 다음과 같이 미분할 수 있습니다.
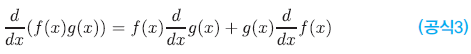
상수는 미분의 밖으로 나올 수 있습니다. k를 임의의 실수로 했을 때, 다음의 공식이 성립됩니다.

그럼 예로서 다음의 함수를 미분해봅시다.

이 함수는 (공식1), (공식2), (공식4)를 조합해서 다음과 같이 미분할 수 있습니다.

이상과 같이 공식을 조합함으로써 여러 가지 함수의 도함수를 구할 수 있습니다.

《처음 만나는 AI 수학 with Python》
'IT 정보' 카테고리의 다른 글
| 인공지능 수학 공부, 꼭 알아야 할 편미분과 전미분! (0) | 2021.02.04 |
|---|---|
| DevOps를 도입하는 조직 체제의 Best Practice는 있는가? (0) | 2021.01.21 |
| AI에 필요한 수학을 공부하고 싶다면? 이 책을 꼭 읽어보세요! (0) | 2021.01.19 |



